Lang (Amy) Zou

she/her | age 16 | Toronto, ON

Divisional Award Intermediate Age Group: Discovery, Inderdisciplinary Award First Place Intermediate, and Best in Age Category, Ottawa Regional Science Fair 2022

Edited by Imogen den Otter-Moore

VIEW PDF

INTRODUCTION

Throughout history, humanity has been fascinated by the persistent circular voids known as impact craters, which provide valuable information about meteorites' dimensions, mass, composition, and age. This study explores the factors influencing the size and depth of these craters, simulating the concept of "meteorites," via hand-crafted marbles that serve as proxies for free-falling bodies interacting with the receptive surface of sand. The result of the investigation analyzes the correlation between crater dimensions (size and depth) and marble density through linear regression graphs, providing a quantitative perspective on the studied density-force relationship.

RESEARCH QUESTION

How do impactor density and drop height influence crater diameter and depth?

BACKGROUND

Meteorites
A meteorite is a relatively small natural object from interplanetary space that survives its passage through Earth's atmosphere and lands on the surface. In modern usage, the term refers to similar objects that land on the surface of other, larger bodies (“Meteorite | Definition, Types, Identification, & Facts | Britannica,” 2023).

Impact Craters
Impact craters are created by the collision of a meteorite with Earth or other planets. When meteorites give a downward force to the ground at high velocity, the pressure and energy pulverize the rocks immediately, and the ejecta falls around to form a circular rim. Craters can be further divided into primary and secondary craters. Primary craters are directly formed by the high-velocity impact of the meteorite. (Crater | National Geographic Society, 2022). Secondary craters are formed by fragments splashed during the hypervelocity impact of the primary crater (Hargitai, 2014).

PHYSICS OVERVIEW

A number of physics concepts were considered in the study of impact craters and how they are formed, for instance, Newton’s three Laws of Motion. The First Law of Motion indicates that an object will accelerate if all forces acting on it are balanced. The Second Law of Motion states that acceleration is proportional to the net force, which is the sum of all forces acting on the object, and inversely proportional to the mass of the object (Newton’s Second Law of Motion, 2022).

F(net) = m • a

Net force is represented by F (net), mass by m, and acceleration by a. The force of gravity has an impact on the acceleration of free-falling objects. When an object is dropped under the gravitational pull, the approximate acceleration due to gravity is 9.8 m/s² (The Acceleration of Gravity, 2022).

Conservation of energy: Kinetic energy is the energy needed for an object to move at a constant speed. Potential energy is a categorized form of energy that is dependent on the relative positions of different system components. In the case of a free-falling object, its potential energy is converted to kinetic energy and then into heat and/or sound energy when it reaches the ground (What Is Kinetic Energy? (Article) | Khan Academy, 2022). In the equation, KE is represented by kinetic energy, velocity squared by v²:

KE = 1/2 m v²

Momentum Equation: Momentum is directly proportional to the velocity and mass of an object; it is a quantity of motion that an object could obtain: The object in motion has momentum. In the equations, the relationship between momentum (p) and velocity (v) is shown in relation to the mass of the falling object.

∵ p = m • v

KE = 1/2 m • v²

Substituting m • p into the equation above, results in:

∴ KE = 1/2 • p • v

Therefore, according to the calculations, the more momentum is given to the object, the more kinetic energy the object will have (Momentum, 2022).

Density is one of the factors that affect the crater's shape and size. Expressed as “rho” (ρ), density is the mass per unit volume. In the equation, density is represented by ρ (rho), volume by V.

ρ = m/v

Terminal Velocity: An object falling through the fluid (air or liquid) experiences two external forces. One is its weight, or the gravitational force (W); the other force is the air resistance, otherwise known as the drag force (D). These two forces are both vector quantities in Newton’s second law of motion, when the relationship of acceleration, net force, and mass is shown below:

∵a = F(net)/m

W and D are opposite forces that cancel each other out:

∴W - D = F(net)

∴ a = (W-D)/M

However, terminal velocity describes the scenario when the drag force equals the gravitational force (W = D), a state in which all free-falling objects will reach acceleration equal to 0, meaning a constant velocity.

D = Cd • r • v² • A/2

In the formula of drag force, Drag (D) depends on a drag coefficient (Cd), the atmospheric density r, the air velocity squared v², and the projected area A of the falling object. The larger the area A, the greater the air resistance, which results in a lower terminal velocity because the Drag force increases with the square of the speed if the air resistance becomes equal to the weight faster, the sooner the acceleration stops (e.g parachute) (Terminal Velocity, 2021) Furthermore, the denser the object is, the greater the force of gravity. This means that the air resistance cancels the W of denser objects slower, and the object continues to accelerate downward.

MATERIALS & METHODS

Variables
In the scope of assessing crater dimensions, the outer rim's size will be characterized by the secondary crater (larger crater). Measurements of crater diameter and depth will be documented in centimeters. The independent variables consist of marble density, the height from which the marble is dropped (cm), the impact of air resistance (R), and gravitational force (g). The dependent variables encompass the impact crater's diameter and depth (cm) and the resultant crater shape. To maintain consistency across trials, the constant variables encompass the mass of the marble (grams), the height from which each marble is released, the angle of release, and the sand tray utilized.

Materials
This experiment uses five marbles, each with a distinct density: Marble 1 (ρ = 3.10g/ml), Marble 2 (ρ = 2.07g/ml), Marble 3 (ρ = 1.77 /ml), Marble 4 ( = 1.55 g/ml), and Marble 5 ( = 1.38 g/ml). A sandstray, two 100cm rulers, a 15cm ruler, a toothpick, a scientific measuring tube, and a precision weighing scale are also required.

Procedure
The experimental protocol proceeded as follows. First, the masses of Marbles 1 to 5 were measured using a precision scale. Subsequently, the volumes of these marbles were determined by employing a scientific test tube. The densities of Marbles 1 and 2 were computed through the formula mass/volume. The experiment was conducted on a sand tray positioned on a level surface. The height from which each marble was to be released was ascertained by using a perpendicular ruler aligned with the sand's horizontal surface. For Marble 1, the initial position was set at 30cm on the ruler, followed by a controlled release from the specified height. After impact, the resultant crater was attentively examined, and the marble was extracted. Subsequently, both the primary and secondary crater diameters were measured, expressed in centimeters. To gauge the crater depth, a toothpick was positioned perpendicular to the crater's base, and the portion extending above the sand surface was measured using a ruler. To prevent interference, the sand tray was leveled before each subsequent trial. The entire sequence, encompassing the previous steps, was repeated at nine incremental drop heights: 45, 60, 75, 90, 105, 120, 135, and 150cm. Following this, Marbles 2 to 5 underwent the same procedures as outlined for Marble 1.

RESULTS

Graph 1 shows the relationship between impactor density and crater size when the marble was dropped from 30 cm.

**Graph 1**: Crater size and depth (cm) over impactor density (g/ml) at 30cm.

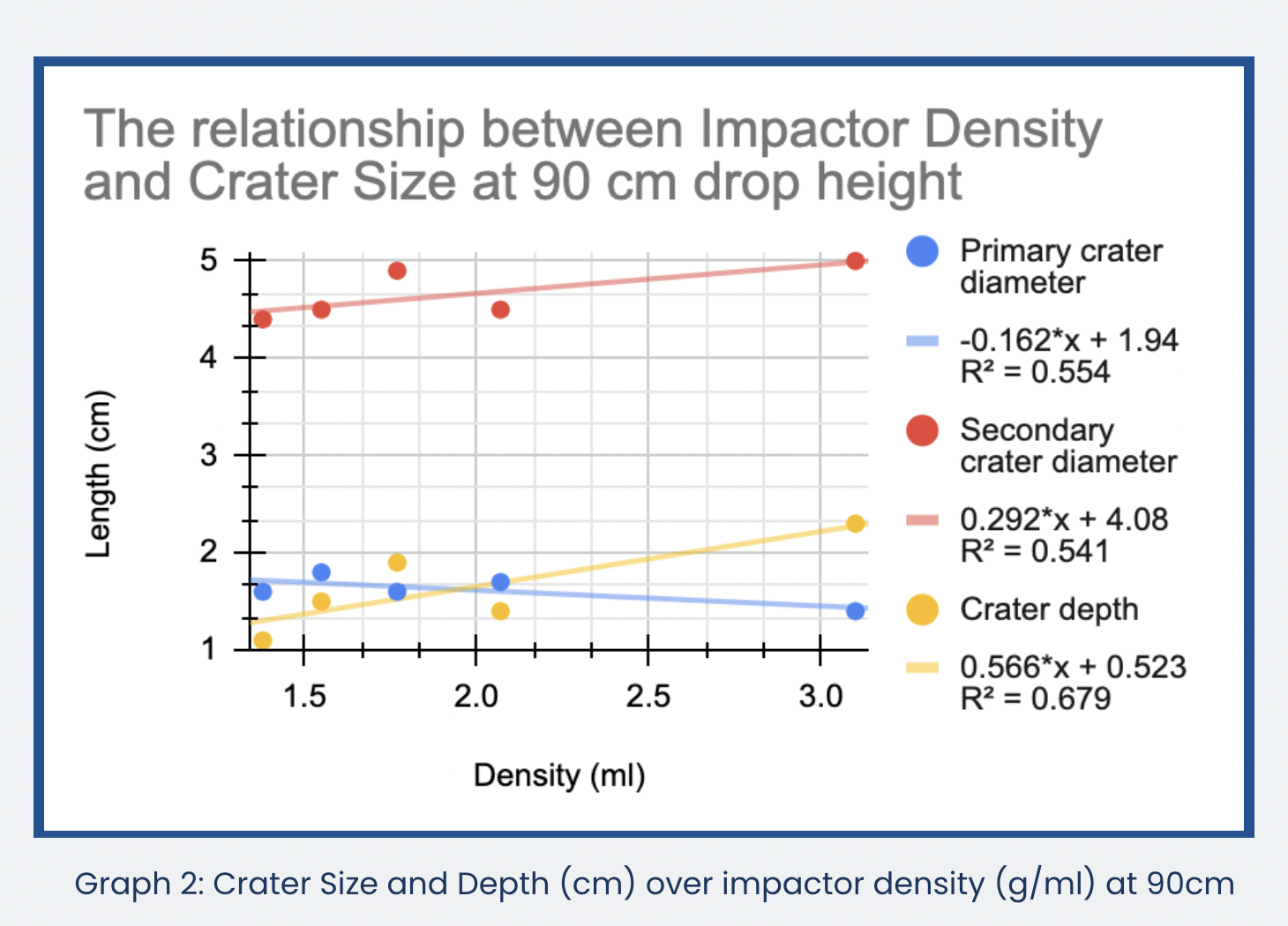
Graph 2 shows the relationship between impactor density and crater size when the marble was dropped from 90 cm.

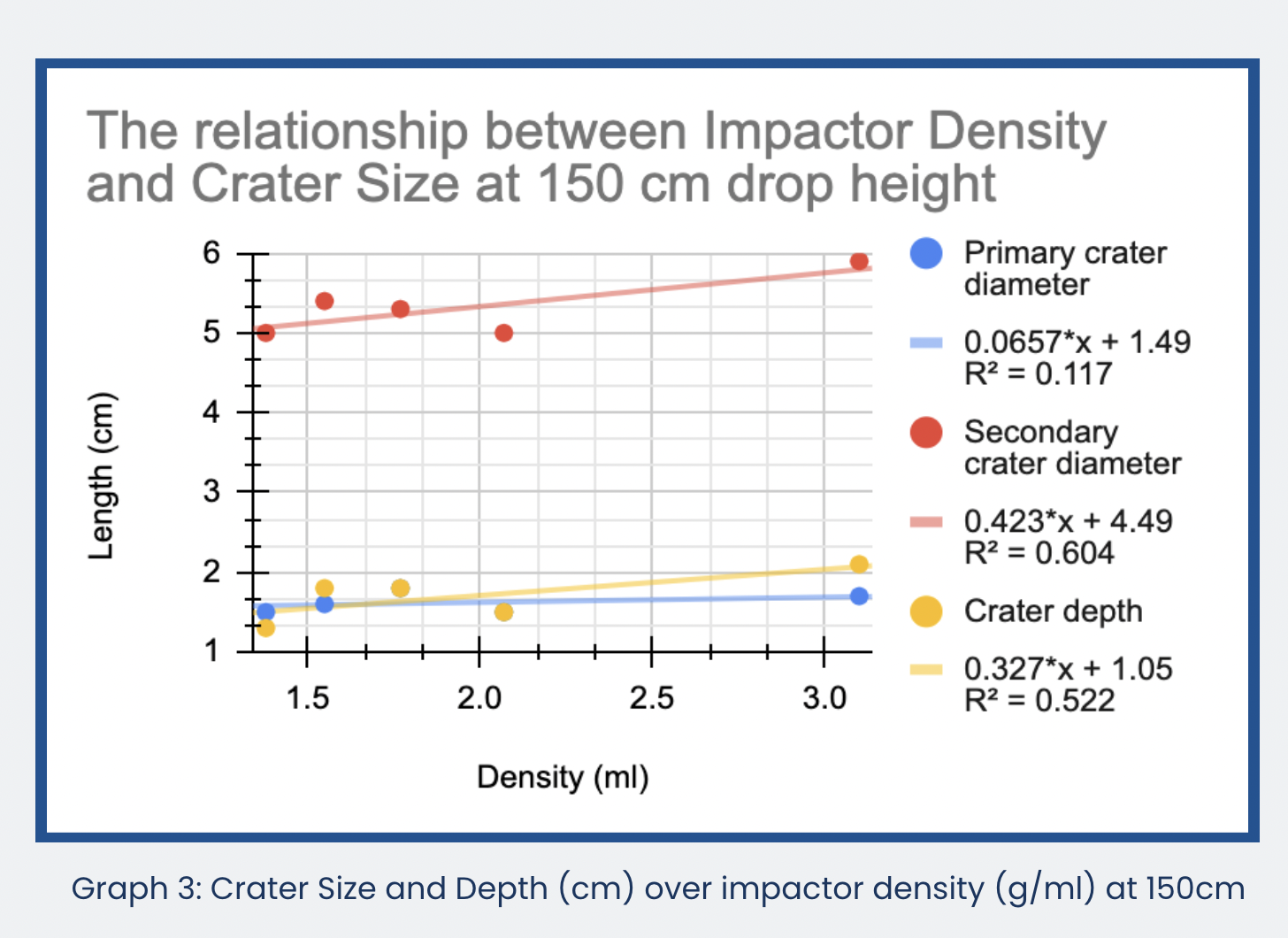
Graph 3 shows the relationship between impactor density and crater size when the marble was dropped from 150 cm.

Graph 4 shows the effect of impactor density on primary impact crater diameter at different drop heights.

Graph 5 shows the effect of impactor density on secondary impact crater diameter at different drop heights.

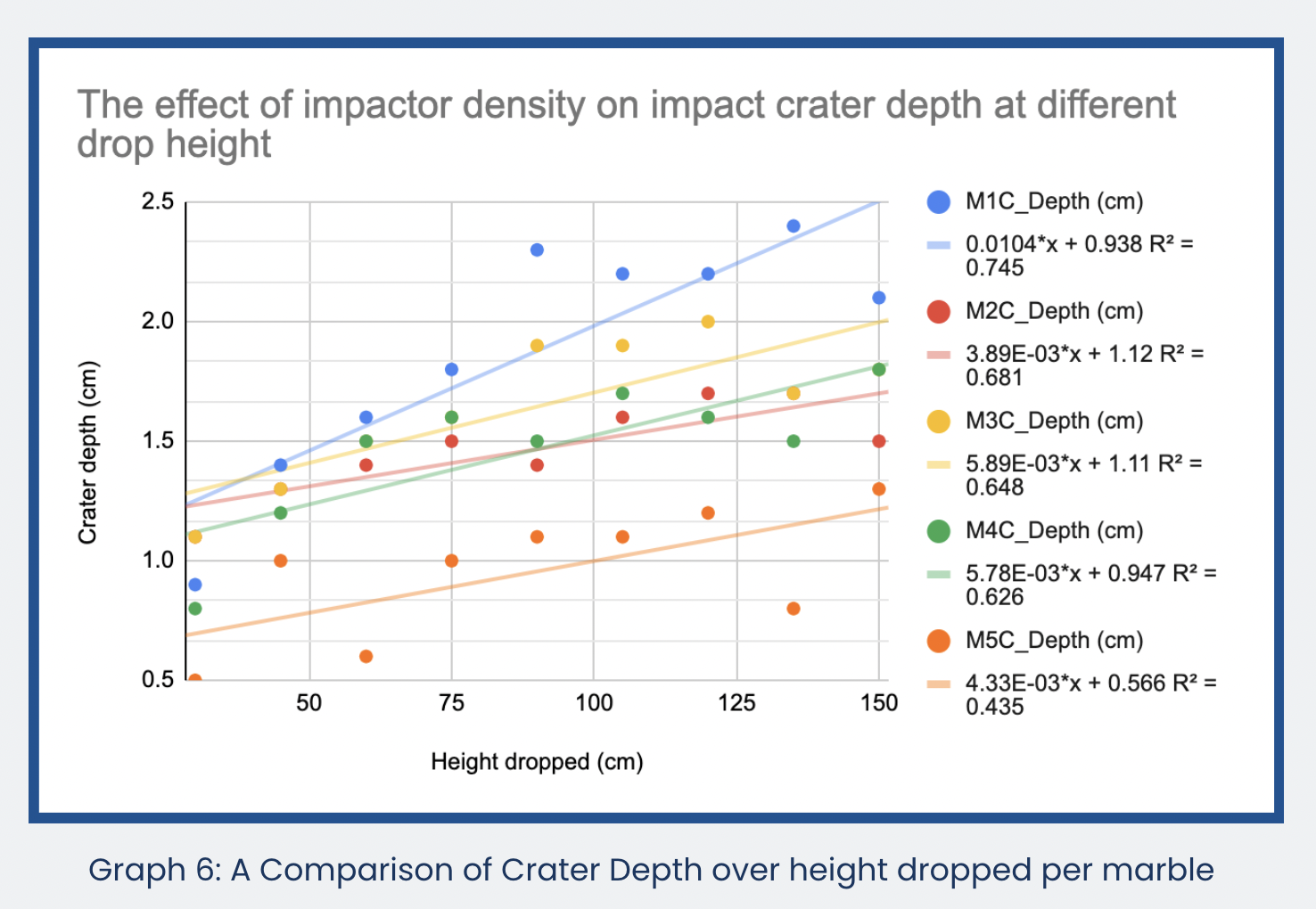
Graph 6 shows the effect of impactor density on impact creator depth at different drop heights.

DISCUSSION

The hypothesis stated that the greater the marble density, the larger and deeper the crater is, because of the distinctive gravitational force and air resistance acting differently on dense marbles. According to the results obtained from the experiment, the hypothesis is partially supported, as can be seen in graphs 1 to 3. Firstly, positive correlations are evident between the secondary crater's diameter and impactor density across all graphs, underscoring the dependence of the ejecta range on the impactor's density. Secondly, the highest slope of 0.566cm/1 density unit occurred in Graph 2, showing the crater depth when the drop height is 90cm increases as the density of marble increases the most. It also has R² = 0.679, which indicates a mediocre level of relevance between the two variables, density and depth. Thirdly, the single negative slope of -0.162 with R² = 0.554 occurred in Graph 2, showing a negative correlation between the primary crater’s diameter and the marble’s density. However, in Graph 3, when marbles were dropped from 150cm, the lowest positive slope of 0.0657 still shows the proportional relationship between primary crater diameter and impactor density.

It can be inferred that the higher the drop height, the smaller the difference between data points, which means that the longer the drop distance, the more predictable the trendline is. Some other observations are made regarding the five marbles specifically. To begin with, both Graphs 5 and 6 show that the secondary crater’s diameter and crater depth in the experiment are directly proportional to the increasing drop height. Marble 1 (ρ = 3.10g/ml), the densest marble has the steepest trendline in graph 6 and the greatest crater depth and secondary diameter. It can be further compared with other flatter trendlines to show that higher density results in a higher force striking in the sand to create a larger crater. Marble 5 (ρ = 1.55 g/ml) has the lowest y-intercept of 2.7cm and 0.5cm at 30cm drop height in graphs 5 and 6, which indicates that the least dense marble creates the least force at the very beginning, even if it does not create the least force resulting in a bigger secondary crater at the end. Furthermore, Graph 5 demonstrates that secondary crater diameters increase at a more constant rate than the crater depth when one compares graphs 5 to 6 with graphs 1 to 3. This is because the R² values in Graphs 5 and 6 are mostly above 0.9, while Graphs 1 to 3 mostly have a R² value below 0.9. As a result, the study partially affirms that density has an influence on crater size to a discernible extent. This infers that denser objects yield greater net forces during crater formation.

EVALUATION

The method used in this experiment is valid for various reasons. First, with regard to variables and experimental design, only one variable was changed at a time during the experiment, which was the marble density. The five marbles are being tested at nine different drop distances to ensure that the experiment covers the more generalized claim that no matter how the drop height changes, the marbles’ density still affects the crater formation in the same way. Moreover, the process of data collection was meticulous, and the craters that took part in the results were carefully selected. Sometimes craters could end up being elliptical due to the positioning of the ruler; therefore, only round-shaped craters are taken as a data point to represent the crater size by measuring their diameters (an estimated number of more than 30 craters were discarded). However, there were also some potential sources of error in this study. While conducting the experiment, the marbles likely experienced friction with the ruler during the free fall, which altered their velocity before striking the sand. Then, when taking the marble out of the crater hole, the shape of the primary crater can be slightly affected. These deviations can be greatly reduced if the ruler is placed outside of the sand tray to minimize its influence. Lastly, marbles were dropped by hand, which means that additional forces could have been unavoidably applied to the marbles. This could possibly cause the velocity at different attempts at different heights to be inconsistent. Unless using mechanical arms to control this variable, no other method could help mitigate this error.

CONCLUSION

This investigation unveils numerous avenues for expanding the experimental scope to delve deeper into the intricacies influencing impact craters. One prospective avenue entails employing a robotic arm to release marbles at varying angles, thereby exploring the impact of different trajectories on the elliptical dimensions of craters upon impact. Furthermore, an exploration of the interaction between marble release angles and sand tray impact could illuminate nuances. Future work could examine how geological conditions at the impact site could influence crater shapes, offering insights into the interplay between impact dynamics and geological contexts. From a material perspective, future investigations could use different materials for each marble, simulating the diversity of extraterrestrial bodies and the elemental composition of meteorites in outer space. In the context of advancing technology and a growing understanding of Earth's intricacies, such as meteoroid-to-meteorite transitions, the significance of studying impact craters becomes evident. These craters serve as important remnants of past cosmic collisions, offering a valuable temporal and celestial perspective. Beyond their historical value, they provide essential data for researchers to model the forces and origins of meteoritic events. With this knowledge, scientists are better equipped to anticipate and prepare for future impact events, enhancing our ability to mitigate potential catastrophic consequences.

REFERENCES

crater | National Geographic Society. (n.d.). Education.nationalgeographic.org. https://education.nationalgeographic.org/resource/crater

dummies - Learning Made Easy. (2023). Dummies.com. https://www.dummies.com/article/academics-the-arts/science/physics/how-to-calculate-th

Encyclopedia Britannica. (2018). Conservation of Energy. In Encyclopædia Britannica. https://www.britannica.com/science/conservation-of-energy

Henrik Hargitai. (2014). Crater. Springer EBooks, 1–2. https://doi.org/10.1007/978-1-4614-9213-9_71-2

Khan Academy. (2022). What is kinetic energy? (article). Khan Academy. https://www.khanacademy.org/science/physics/work-and-energy/work-and-energy-tutorial/a/what-is-kinetic-energy

Momentum. (n.d.). Www.physicsclassroom.com. Retrieved September 10, 2023, from https://www.physicsclassroom.com/Class/momentum/u4l1a.cfm#:~:text=In%20terms%2

NASA. (2018). Terminal Velocity. Nasa.gov. https://www.grc.nasa.gov/WWW/K-12/airplane/termv.html

Newton’s Second Law of Motion. (n.d.). Www.physicsclassroom.com. Retrieved September 10, 2023, from https://www.physicsclassroom.com/class/newtlaws/Lesson-3/Newton-s-Second-Law#:~:t

The Acceleration of Gravity. (n.d.). Www.physicsclassroom.com. Retrieved September 10, 2023, from https://www.physicsclassroom.com/class/1DKin/Lesson-5/Acceleration-of-Gravity#:~:te

Cratering, Impactors and Ejecta